
In 2020, the IOG team published the work One-shot Signatures and Applications to Hybrid Quantum/Classical Authentication. The work went unnoticed. It was known only in the Cardano community. The Ethereum team recently came across this work and is excited about it. A collaborative workshop between the University of Edinburgh, IOG, and the Ethereum team is planned. One-shot signatures bring advanced cryptography to better secure the functioning of the blockchain. In addition, it allows the creation of such things as blockchain-less cryptocurrency. In the article, we will explain the basic principles of one-shot signatures. Then we will explain how this technology can significantly improve the security of Cardano.
Hybrid System
The one-shot signatures scheme is a hybrid system that combines principles from quantum mechanics with classical communication methods.
Classical communication methods include traditional internet technologies for transferring data (protocols) and classical cryptographic schemes, such as public key cryptography.
So, while the system allows for local quantum operations (more details later), the actual transmission of information is done using these classical methods. This approach allows for the implementation of quantum principles in a way that is compatible with existing technologies.
The system utilizes the quantum no-cloning principle, which is a fundamental postulate of quantum mechanics stating that it is impossible to create an identical copy of an arbitrary unknown quantum state.
This principle ensures that once a secret key is used, it cannot be cloned or reused. This is a key aspect of the security provided by one-shot signatures. Any secret key can be used to sign only a single message. Then the key self-destructs. This cannot be achieved in classical cryptography.
In classical cryptography, the owner of the secret key (private key) can sign as many messages as he wants. There is no way to prevent multiple messages from being signed (a possible mitigation can be achieved through some system of counters and timestamps defining the order of messages) or to prevent key sharing between multiple people.
The one-shot signatures system is a kind of mathematical system that incorporates principles from quantum mechanics to provide enhanced security features. But it’s also a hybrid system that combines these quantum principles with classical communication methods.
Understanding Quantum No-cloning Principle
I have no ambition to explain quantum mechanics in detail. Fortunately, you only need to understand the quantum no-cloning principle. The one-shot signatures system uses the principle but implements it through classical methods.
Let’s explain the quantum no-cloning principle with a simple example.
Imagine you have a magical box that can create a unique kind of candy every time you open it. Each candy has a special flavor that you’ve never tasted before.

Now, suppose you liked one of the candies and wanted to make an exact copy of it.
In the world of quantum mechanics, this is like trying to clone a quantum state. But here’s the catch: the ‘no-cloning principle’ says that you can’t make an exact copy of that candy. No matter how hard you try, you can’t recreate the same flavor again.
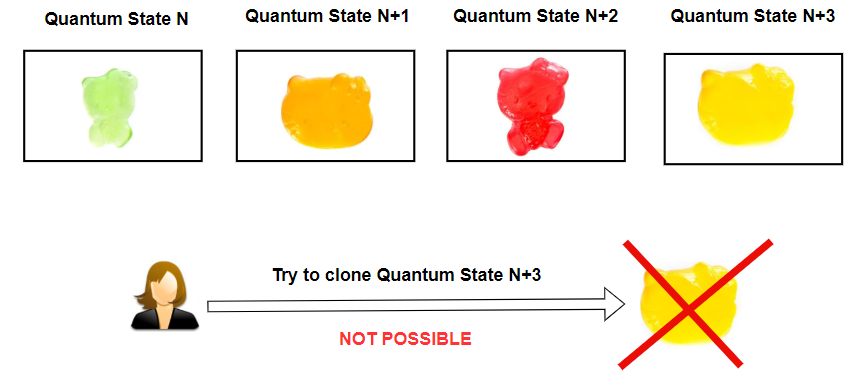
In the context of one-shot signatures, this principle is used to ensure that once a secret key (think of it as the special candy) is used, it cannot be copied or used again. This makes the system very secure because no one else can recreate your special candy (or secret key).
In the image below, each key in the magical box is unique (non-clonable).
In the candy analogy, the ‘magical box’ can be thought of as a quantum system, and the creation of a unique kind of candy can be seen as a local quantum operation.
As you will see later, the local quantum operation is part of the process during the interaction between the participants.
In real quantum systems, a local quantum operation could be something like preparing a quantum state or performing a measurement on a part of the system. These operations are ‘local’ because they’re performed on individual parts of the quantum system, independently of other parts.
For example, imagine you have two magical boxes (two parts of a quantum system). You could open one box to create a candy (perform a local quantum operation), without affecting the other box at all. This is what we mean by ‘local’ in local quantum operations.
In the context of quantum cryptography, these local quantum operations are used to manipulate quantum information, such as the secret keys used in one-shot signatures.
Using A One-shot Signatures System
I will show you an example that best demonstrates the power of the one-shot signatures system, as it enables an interaction between Alice and Bob that is unattainable through classical cryptography.
Consider the task of signature delegation. Alice wishes to allow Bob to sign a single message on her behalf. Carol has the public key to verify the message.
Alice could just give Bob her secret key, but this would allow Bob to sign any number of messages.
In the image below, you can see how the scenario would look using classic cryptography. Alice would share the secret key with the Bot. Bob could sign the message. Carol would use the verification (public) key to verify the authenticity of the message.
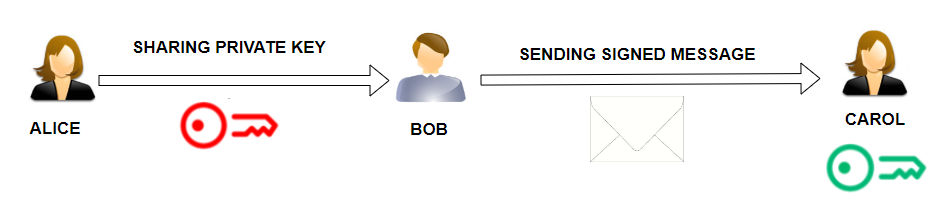
Alice instead wants to give Bob enough information to ensure that Bob can subsequently sign a single arbitrary message, without any further action on Alice’s part. Crucially, we want the message to only be decided after Alice hands this information to Bob.
Of course, as shown above, this task is impossible in a purely classical world, as Bob can re-use whatever information he learned from Alice. In traditional public key cryptography, a single private key can be used to sign multiple messages.
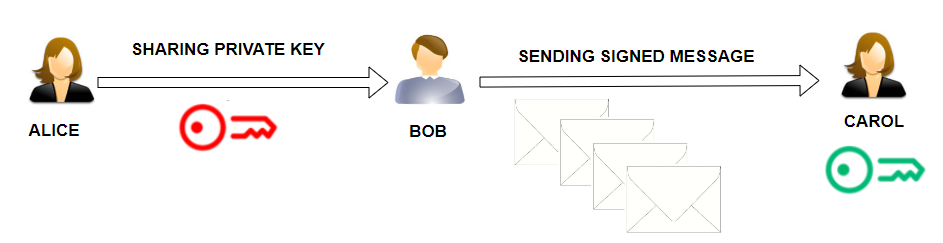
One could hope that Alice could provide Bob with a quantum signing token, which self-destructs after signing a message. By quantum no-cloning (which says that general unknown quantum states cannot be copied) Bob cannot copy the token, and therefore can only sign a single message.
In the picture, you can see that Alice creates a quantum token that she sends to Bob. Bob can sign only one message using the token. The token is subsequently self-destructed. Bob cannot sign another message.
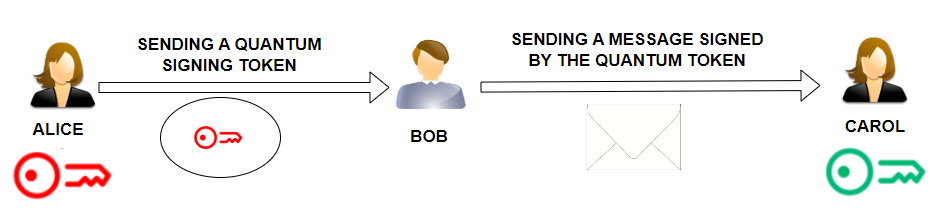
Note that Alice must be able to pass the cryptographic secret to Bob in a specific way. Bob must not be able to clone cryptographic secrets. He can only use it once, i.e. perform a one-shot signature of the message. A quantum signing token was used to pass the cryptographic secret.
Alice can create a secret key (which is represented by a quantum state) and pass it to Bob. This secret key can then be used by Bob to sign a single message on Alice’s behalf.
However, it’s important to note that neither Alice nor Bob can know the exact value of the key.
This is due to the quantum no-cloning principle, which states that it is impossible to create an exact copy of an arbitrary unknown quantum state.
So, while Alice and Bob can use the key for signing and verifying messages, they cannot see or clone the key.
Once Bob uses the secret key to sign a message, the key self-destructs and cannot be used again. This ensures the security of the system, as it prevents any potential misuse of the secret key.
This is the essence of the innovation brought by the one-shot signatures system.
We will return to this scenario later when we explain local quantum operations.
Interaction between Alice and Bob
With one-shot signatures, it’s possible that the same public key could be associated with multiple private keys, each of which can be used once for signing.
However, the specifics of how the public and private keys are generated and used would depend on the particular implementation of the one-shot signatures system.
For concrete use cases, it may be important to ensure that participants are limited in their ability to produce new cryptographic secrets (for example, quantum tokens). The effect could be similar to reusing the same private key over and over again.
Generally, in cryptographic systems, mechanisms are put in place to ensure the integrity and authenticity of the signatures. These mechanisms could include the use of timestamps, sequence numbers, or other forms of record-keeping that track the usage of the secret keys.
As explained in the introduction, the one-shot signatures scheme is a hybrid system using the principle of quantum mechanics, but fully implemented through classical cryptographic schemes (and using internet protocols to allow communication between participants).

Classical cryptographic schemes refer to traditional methods of encrypting and decrypting information, such as symmetric key algorithms (where the same key is used for encryption and decryption) and asymmetric key algorithms (where different keys are used for encryption and decryption).
Classical cryptography is used to perform local quantum operations.
The interaction between Alice and Bob is fully implemented using classic methods. However, a key part of the interaction process is the creation (emulation) of the quantum state.
Local quantum operation refers to quantum operations that are performed locally, i.e., on individual parts of the quantum system, as part of the one-shot signature scheme.
In a typical scenario, one party performs a local quantum operation on their part of the quantum system. The results of this operation are then communicated to the other party using classical communication. Based on this information, the second party may then perform their local quantum operation.
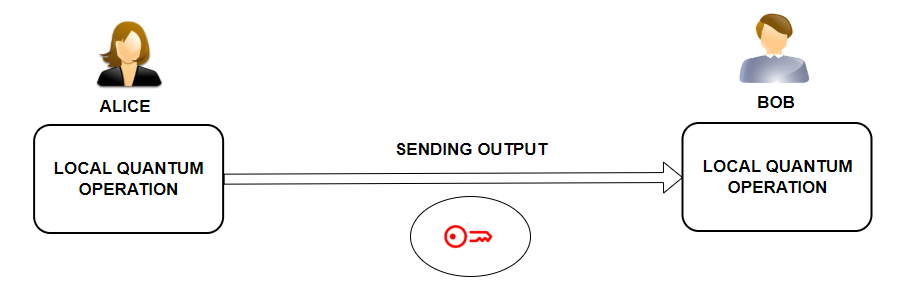
In the one-shot signatures system, the parties manipulate and exchange quantum information. They perform local quantum operations as part of the signature scheme, with the results being communicated classically.
Here’s a simplified step-by-step process:
- The sender performs a local quantum operation on their part of the quantum system. This operation could involve preparing a quantum state or performing a measurement.
- The sender then communicates the result of this operation to the receiver using classical communication.
- Upon receiving this information, the receiver can then perform their local quantum operation. This operation could be conditioned on the information received from the sender.
- The receiver’s operation could involve verifying the sender’s message, decoding information, or performing some other task relevant to the protocol.
Non-clonable Keys
The concept of non-clonable keys in quantum cryptography is closely related to the no-cloning theorem in quantum mechanics.
This means that once a quantum state (which could represent a secret key) is used, it cannot be cloned or copied. This provides a fundamental level of security, as it prevents any potential eavesdropper from making a copy of the quantum state and thereby gaining access to the secret key.
Let’s now return to the scenario from the beginning of the article when Alice wanted to delegate to Bob the right to sign a message on her behalf. We will explain how a quantum signing token is created.
Alice can create a secret key (which is represented by a quantum state) and pass it to Bob. This secret key can then be used by Bob to sign a single message on Alice’s behalf.
Recall that neither participant knows the value of the key.
Once Bob uses the secret key to sign a message, the quantum state is no longer valid for further use. Thus, it is not possible to make a copy.
In quantum terminology, it is said that the quantum state ‘collapses’ when a measurement is made. The act of using the secret key to sign a message can be thought of as a kind of measurement, causing the quantum state to collapse. After this collapse, the quantum state (i.e., the secret key) cannot be used again.
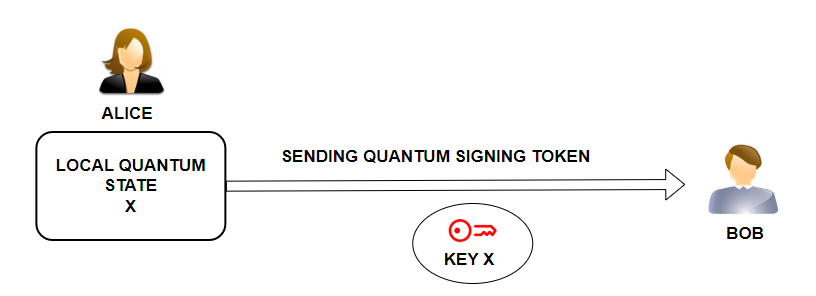
Now let’s go through the scenario step by step. We will show how a secret key is created and subsequently self-destructed.
Alice performs a local quantum operation (quantum state X) during which the private key X is created. Alice sends the key X to Bob in a quantum signing token (a box that protects the value of the key X).
Bob performs a local quantum operation (quantum state Y) during which the message is signed. The input for this operation is a quantum signing token containing a private key X. The output of the operation is a message signed by private key X. The message signature initializes the collapse of the quantum state.
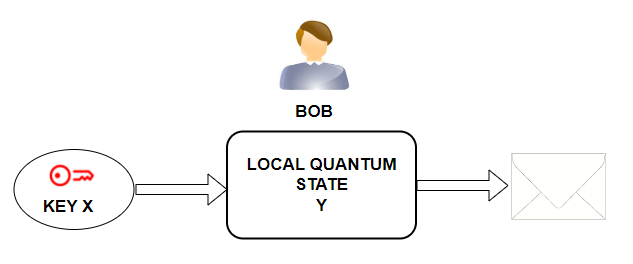
At the moment when Bob signs the message with the private key X, the quantum state X collapses, i.e. also the private key X self-destructs.

At this point in the scenario, it is not possible to clone the private key X or use it again. No one has ever known its value and will never know. The result is a signed message.
I hope you now understand the concept of non-clonable keys.
Forward security and KES
Forward security is a property of cryptographic systems that ensures that the compromise of the current key does not compromise the secrecy of past sessions because other keys were used.
In other words, even if an adversary can obtain a decryption key, they cannot use it to decrypt past communications. This is because each session uses a unique key, which is deleted or updated after use.
A similar principle is used in Cardano for signing blocks.
If the secret key of an SPO is compromised at some point in time, the signatures generated before that point remain valid and unforgeable.
This is achieved by dividing the lifetime of the signer into periods and using a different secret key for each period. The secret key for each period is derived from the previous one, and then erased after use. The public key remains the same for all periods.
KES limits the scope of each secret key to a specific period (currently 90 days) and ensures that old secret keys are erased and unrecoverable. Therefore, even if an adversary obtains a secret key for a certain period, they can only forge signatures for that period, and not for any previous or future periods.
If an adversary obtains the signing keys of a single operator, he can overwrite only those blocks that were minted by this operator in the period when the key was active. This can be a relatively small number of blocks. Slot leaders are drawn randomly based on their stakes. There are a large number of SPOs in the Cardano network. For an adversary to have a chance to compromise Cardano, he would need to obtain not just a single key, but many keys from a large number of SPOs.
One way to get signing keys is to steal them from SPOs. If SPOs delete old keys, they cannot be stolen. However, the deletion of keys cannot be forced. SPOs can theoretically keep the old keys.
The OSS system can prevent the execution of attacks, as there will be no keys that could be misused. Each new block will be signed with a unique key that will be created for one-time signature only.
Using One-shot Signatures To Secure Cardano
One-shot signatures can be used to implement ordered signatures, i.e. a specific mechanism in which it is possible to determine the validity of a sequence of messages or blocks.
The OSS system is a type of signature where any secret key can be used to sign only a single message and then self-destruct. This concept is particularly useful in the context of blockchain technology, where maintaining the integrity and order of blocks is critical.
The order of blocks is crucial because it determines the state of the blockchain at any given point in time. If the order of blocks were changed, it would result in a different state of the blockchain.
Digital signatures play a key role in maintaining this order. When a new block is created, it is signed by the creator of the block. This signature serves as a seal that verifies the authenticity of the block and its position in the chain.
Using a unique key for each signature can provide an additional layer of security. Since each key can only be used once, it becomes impossible to reuse a key to sign a different block or to alter the order of existing blocks. With OSS, it is not possible to overwrite the history of the Cardano ledger.
So, in essence, the ordered sequence of one-shot signatures can help users deterministically identify which blocks are valid and which ones are not, thereby ensuring the integrity and order of the blockchain.
You can think of ordered signatures like a series of locked boxes, each containing a unique key. These boxes are arranged in a specific order. The key in each box can only be used once to unlock the next box in the series, and then it self-destructs. This means that each secret key (or unique key in the box) can be used to sign only a single message. The order of the signatures is determined by the sequence of the boxes.
In the context of KES, ordered signatures can be seen as a sequence of keys that are used in a specific order for signing. Each key in this sequence can be used only once, and then it self-destructs. This means that even within the same period, different keys would be used to sign different blocks. Not just a single key for a given period as it is today.
This change could potentially enhance the security of the Cardano network by making it more resistant to certain types of attacks. For example, it could help prevent long-range attacks, where an attacker tries to rewrite the history of the blockchain by using old keys.
Let’s explain the basic concept of how ordered signatures work.
When a party signs a message, he also specifies a tag t. The signing key allows for signing any message, but the requirement is that messages can only be signed in order of increasing t. That is, once a message is signed at tag t0, it then becomes impossible to sign a message at a past tag (t1 < t0). So, every message is signed concerning a tag t.
The public key will be the public key for a one-shot signature scheme.
To sign a message at tag t, it is necessary to construct a new one-shot signature public and private key pair and delegate it to the new public key. When signing to delegate, sign the entire public key/tag/message triple.
The signature consists of the entire signature chain from the original public key to the latest public key.
Verification requires verification of the signature chain as well as that the tags in the chain occur in increasing order.
The idea is that the only way to produce a new signature is to append it to the signature chain.
Therefore, once an adversary produces a signature at tag t0, he has committed to all the signatures he will produce at tags t1 < t0. If he tries to sign a different message at t1, this will constitute a fork in the chain, violating the one-shot security property.
How Would OSS Prevent Attacks On Cardano?
At the moment, no details are known about how the OSS system could be implemented. Nevertheless, it is possible to assume how such a system could work.
As explained in the previous section, the system can work with tags. Tags can define the sequence number of a block. When signing a new block, it will be necessary to increment the tag (sequence number).
When a block is signed and a tag is incremented, a unique identifier is generated. This unique identifier is associated with the specific combination of the block (the block could be represented by a hash), signature, and tag.
Let’s try to explain it with a simplified example.
Imagine you’re playing a game of building blocks with your friends (you are SPOs). Each of you has a unique set of blocks and you’re building a tower together. Each block represents a set of transactions or a piece of data, and the tower represents the blockchain.
One-shot signatures are like unique stickers that each of you puts on your block when you add it to the tower. This sticker is so special that it can only be used once and then it disappears (the key self-destructs). It’s made using a secret key, which is like a magic wand. But here’s the catch — the magic wand can only create one sticker and then it breaks.
Now, let’s say you want to make sure that the blocks (or transactions) are added to the tower (or blockchain) in the right order. This is where tags and unique identifiers come in.
Each sticker (or signature) you create with your magic wand (or secret key) has a unique tag or identifier. This tag could be a number or a code that is different for each sticker. When you put your block on the tower, everyone can see the tag on your sticker and know exactly where it fits in the sequence.
So, if someone tries to move the blocks around or add a block in the wrong place, you would know because the tags on the stickers would be out of order. This is how ordered signatures can help ensure the correct sequence of blocks in a blockchain.
And what about the magic wands (or secret keys)? Well, after you use your wand to create a sticker, it breaks (or self-destructs). This means that even if someone finds your broken wand, they can’t use it to make a new sticker or mess up the order of blocks in the tower.
You can ask what stops someone from using different magic wands (keys) to build a different tower (blockchain) with the same or similar order of blocks (sequence of tags).
Creating a different blockchain that matches the order of the original one is not as simple as it sounds.
Each magic wand (key) is unique and can only create a sticker (signature) for a specific block. So, an adversary can’t just use a different wand to create a sticker for a block that already has one.
In a long-range attack, an adversary tries to create a different blockchain starting from some point in the past. This is like trying to build a different tower starting from the middle. But remember the stickers (signatures) from the past blocks are already there and can’t be changed. So, the adversary can’t just replace them with new ones.
In a blockchain, the order of blocks is determined by a consensus mechanism. This is like a rule in our game that says the order of blocks in the tower is decided by all players together. So, an adversary can’t change the order of blocks on their own.
Conclusion
One-shot signatures have numerous applications including one-time signature tokens (our example), quantum money, decentralized blockchain-less cryptocurrency, signature schemes with unclonable secret keys, non-interactive certifiable min-entropy, and more. The one-shot signatures system is a powerful new building block for novel quantum cryptographic protocols.
The IOG team created one-shot signatures to improve the security of Cardano. The system can help prevent long-range attacks in PoS networks by ensuring that any secret key can be used to sign only a single block and then self-destruct. Cardano can provide stronger security guarantees by replacing the KES mechanism with one-shot signatures. An adversary cannot use old secret keys to rewrite the full history of the blockchain because these keys will not exist after signing the blocks.
Once OSS is implemented in Cardano, security guarantees will be significantly higher. To commit a long-range attack will be almost unthinkable. An adversary cannot obtain keys that were self-destructed immediately after signing the blocks.
The Hidden Gem of IOG: Securing Cardano with One-Shot Signatures was originally published in The Dark Side on Medium, where people are continuing the conversation by highlighting and responding to this story.
from The Dark Side - Medium https://ift.tt/nHzSNY5
0 Comments